RUBY
선형검색, 보초법 (파이썬) 본문
선형검색
선형 검색(Linear Search)
다른이름으로 순차 검색(Sequential Search) 이라고도 한다.
선형 검색은 데이터가 모인 집합(배열, 링크드리스트 등)의 처음부터 끝까지 하나씩 순서대로 비교하며 원하는 값을 찾아내는 알고리즘이다.
→ 순차적으로 검색
| 3 | 5 | 2 | 1 | 0 | 9 | 7 | 8 | 6 | 4 |
데이터를 정렬하거나 따로 건드릴 필요가 없고, 난이도가 쉬운 편이나, 데이터의 양이 많아지면 검색에 소요되는 시간도 비례하여 많아지고, 하나씩 일일이 비교하기 때문에 비효율적이라는 단점이 있다. 예를들어 위와 같은 데이터의 집합이 있을경우 4를 찾으려면 10번의 비교를 거쳐야 한다. 100만개의 데이터가 있고 찾고자 하는 데이터가 100만번째에 있다면 100만번의 비교를 해야 한다는 뜻이다. 이와 같은 상황을 Worst Case라고한다다. 관련된 용어로 평균적인 상황을 Average Case 좋은 상황을 Best Case라고 한다.
datas = [3, 2, 5, 7, 9, 1, 0, 8, 6, 4]
print(f'datas: {datas}')
print(f'datas length: {len(datas)}')
searchData = int(input('찾으려는 숫자 입력: '))
searchResultIdx = -1
n = 0
while True:
if n == len(datas):
searchResultIdx = -1
break
elif datas[n] == searchData:
searchResultIdx = n
break
n += 1
print(f'searchResultIdx: [{searchResultIdx}]')datas: [3, 2, 5, 7, 9, 1, 0, 8, 6, 4]
datas length: 10
찾으려는 숫자 입력: 9
searchResultIdx: [4]
보초법 (Sentinel method)
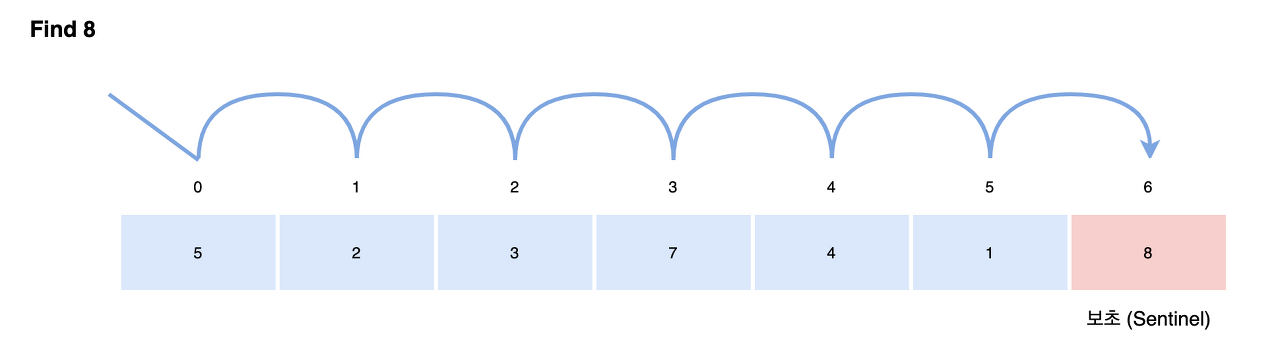
보초 법이란 반복의 종료를 알리는 특정한 값인 보초(Sentinel) 값을 사용하여 종료 조건중 검색 실패 조건을 제거하여 판단 횟수를 줄이는 방법입니다.
검색하고자 하는 키 값을 기존 리스트의 맨 끝 자리에 추가하고 이를 보초 값으로 사용합니다.
이렇게 하면 리스트에 찾던 값이 없어도 보초 값까지 검색하면 "종료 조건 1(검색 실패)"을 만족하게 됩니다.
이렇게 보초는 반복문에서 종료 판단 횟수를 줄이는 역할을 하게 됩니다.

datas = [3, 2, 5, 7, 9, 1, 0, 8, 6, 4]
print(f'datas: {datas}')
print(f'datas length: {len(datas)}')
searchData = int(input('찾으려는 숫자 입력: '))
searchResultIdx = -1
datas.append(searchData)
n = 0
while True:
if datas[n] == searchData:
if n != len(datas) - 1:
searchResultIdx = n
break
n += 1
print(f'datas: {datas}')
print(f'datas length: {len(datas)}')
print(f'searchResultIdx: [{searchResultIdx}]')datas: [3, 2, 5, 7, 9, 1, 0, 8, 6, 4]
datas length: 10
찾으려는 숫자 입력: 9
datas: [3, 2, 5, 7, 9, 1, 0, 8, 6, 4, 9]
datas length: 11
searchResultIdx: [4]
리스트에서 가장 앞에 있는 숫자 ‘7’을 검색하고 위치(인덱스)를 출력하자.
nums = [4, 7, 10, 2, 4, 7, 0, 2, 7, 3, 9]
nums = [4, 7, 10, 2, 4, 7, 0, 2, 7, 3, 9]
print(f'nums: {nums}')
print(f'nums length: {len(nums)}')
searchData = int(input('찾으려는 숫자 입력: '))
searchResultIdx = -1
nums.append(searchData)
n = 0
while True:
if nums[n] == searchData:
if n != len(nums) - 1:
searchResultIdx = n
break
n += 1
print(f'nums: {nums}')
print(f'nums length: {len(nums)}')
print(f'searchResultIdx: [{searchResultIdx}]')
if searchResultIdx < 0:
print(f'찾으려는 {searchData}가(이) 없습니다.')
else:
print(f'찾으려는 {searchData}의 위치(인덱스)는 {searchResultIdx}입니다.')nums: [4, 7, 10, 2, 4, 7, 0, 2, 7, 3, 9]
nums length: 11
찾으려는 숫자 입력: 7
nums: [4, 7, 10, 2, 4, 7, 0, 2, 7, 3, 9, 7]
nums length: 12
searchResultIdx: [1]
찾으려는 7의 위치(인덱스)는 1입니다.
리스트에서 숫자 ‘7’을 모두 검색하고 각각의 위치(인덱스)와 검색 개수를 출력하자
nums = [4, 7, 10, 2, 4, 7, 0, 2, 7, 3, 9]
nums = [4, 7, 10, 2, 4, 7, 0, 2, 7, 3, 9]
print(f'nums: {nums}')
print(f'nums length: {len(nums)}')
searchData = int(input('찾으려는 숫자 입력: '))
searchResultIdxs = []
nums.append(searchData)
n = 0
while True:
if nums[n] == searchData:
if n != len(nums) - 1:
searchResultIdxs.append(n)
else:
break
n += 1
print(f'nums: {nums}')
print(f'nums length: {len(nums)}')
print(f'searchResultIdxs: {searchResultIdxs}')
print(f'searchResultCnts: {len(searchResultIdxs)}')nums: [4, 7, 10, 2, 4, 7, 0, 2, 7, 3, 9]
nums length: 11
찾으려는 숫자 입력: 7
nums: [4, 7, 10, 2, 4, 7, 0, 2, 7, 3, 9, 7]
nums length: 12
searchResultIdxs: [1, 5, 8]
searchResultCnts: 3'프로그래밍 언어 > Python' 카테고리의 다른 글
| 순위Rank (파이썬) (0) | 2023.01.25 |
|---|---|
| 이진 검색(탐색) (파이썬) (0) | 2023.01.25 |
| 딕셔너리를 이용한 프로그래밍(파이썬) (0) | 2023.01.24 |
| 튜플을 이용한 프로그래밍(파이썬) (0) | 2023.01.24 |
| 리스트를 이용한 프로그래밍(파이썬) (0) | 2023.01.24 |

