RUBY
[통계]확률 이론 본문
통계
3. 확률 이론
통계학에서 사용하는 확률 변수의 개념 설명
1. 확률
확률(probability)
- 모든 경우의 수에 대한 특정 사건이 발생하는 비율이다. 대체로 수학 외에서는, 0과 1 사이의 소수 혹은 분수나 순열 등으로 나타내기 보다는, 다른 비율을 나타낼 때처럼 0과 1 사이의 확률에 100을 곱하여 0과 100 사이의 백분율(%)로 나타내거나 옛날처럼 할·푼·리로 나타내기도 한다.
확률의 고전적 정의
- 어떤 사건의 발생 확률은 그것이 일어날 수 있는 경우의 수 대 가능한 모든 경우의 수의 비이다. 단, 이는 어떠한 사건도 다른 사건들보다 더 많이 일어날 수 있다고 기대할 근거가 없을 때, 그러니까 모든 사건이 동일하게 일어날 수 있다고 할 때에 성립한다. (확률의 최초의 정의는 수학자 라플라스의 논문 Théorie analytique des probabilités)
표본 공간(Sample Space)
- 표본 공간이란 어떤 실험에서 나올 수 있는 모든 가능한 결과들의 집합
- 동전 던지기의 경우 S = {앞면, 뒷면}, 주사위던지기 S = {1,2,3,4,5,6}
사건 A가 일어날 확률을 P(A)라고 하고, 표본 공간(S)가 유한집합일때 표본 공간의 모든 원소들이 일어날 확률이 같으면
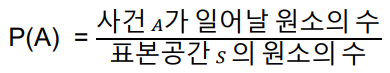
1) 주사위를 던저서 6이 나올 확률
2) 트럼프 카드 52장중 A가 나올 확률
3) 로또 1등에 당첨될 확률
4) 동전 두개를 던져서 뒷면이 한번만 나오는 확률을 얼마인가?
표본공간 S = {(앞, 앞), (뒤, 뒤), (앞, 뒤), (뒤, 앞)}
사건 A = {(앞, 뒤), (뒤, 앞)}
P(A) = 2/4 = 1/2
통계적 확률 정의

1) 타자가 타석에서 안타를 칠 확률
2) 공정에서 제품이 정상일 확률(수율)
확률의 성질
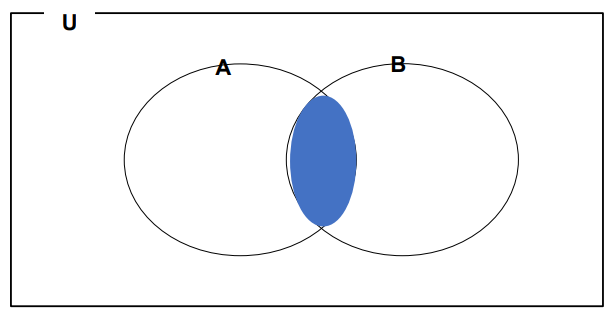
| 합사건(union) 사건 A 또는 사건B가 일어날 확률 A ∪ B |
곱사건(intersection) 사건 A와 사건B가 동시에 일어날 확률 A ∩ B |
 |
 |
| 배반사건(mutually exclusive event) 사건 A와 사건B가 동시에 일어날 수 없을 경우 A ∩ B = ∮ |
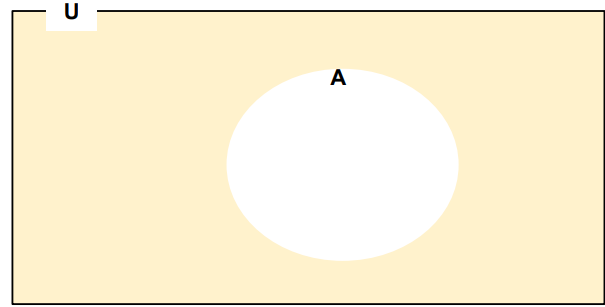
여사건(complement) 사건A가 일어나지 않을 확률 Ac∪ |
 |
 |
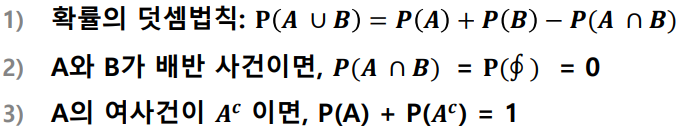
예제 3.2) 1부터 13까지 13장의 카드에서 한장을 뽑는 실험에서 아래의 사건을 생각해보자
A: 짝수를 뽑을 확률
B: 5이하의 카드를 뽑을 확률
(a) 표본공간을 정의하고 각 사건의 확률을 구하라
(b) A와 B의 곱사건과 합사건을 구하라
풀이
(a) S = {1,2,3,4,5,6,7,8,9,10,11,12,13} , P(1) = P(2) = … = P(13) = 1/13
(b) 사건 A는 {2,4,6,8,10,12} P(A) = 6/13 , 사건B는 {1,2,3,4,5} P(B) = 5/13
A ∩ B = {2,4} , P(A ∩ B) = 2/13
P(A ∪ B) = P(A) + P(B) - P(A ∩ B) = 6/13 + 5/13 - 2/13 = 9/1
조합과 순열
- ! (Factorial): n개를 일렬로 늘여 놓은 경우의 수를 n!로 표현하며,
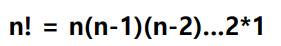
- 순열(Permutation): 순서를 고려하여 n개 중 r개를 뽑아서 배열하는 경우의 수
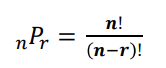
- 조합(Combination) : 순서를 고려하지 않고 n개중 r개를 뽑아서 배열하는 경우의 수
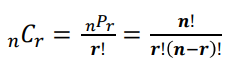
예제 3.3) 로또 1등의 확률과 2등의 확률을 구하시오
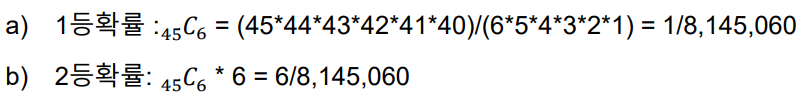
조건부확률(conditional probability)
- 어떤 사건 A가 발생한 상황에서(주어졌을 때) 또 하나의 사건 B가 발생할 확률임
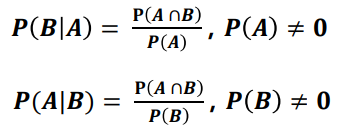
확률의 곱셈법칙

베이즈 정리(Bayes’ Theorem)

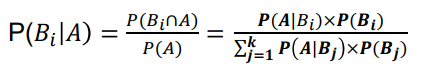
예제 3.4) 자동차 보험의 고객의 분포 A등급 30%, B등급 50%, C등급 20%이고, 각 고객 등급별로 1년내 사고의 확률은
A등급 0.1 B등급 0.2 C등급 0.3이라면
a) 임의의 한 고객을 선택했을때, 그 고객이 1년 이내에 사고를 낼 확률을 구하시오
b) 어떤 고객이 1년내 사고를 낸 고객이라면, 그 고객이 A등급일 확률을 구하시오
풀이) A등급 고객을 4 , 6등급 4 , U등급 4S 라고 하고 1년이내 사고 낼 사건을 B라고 하면
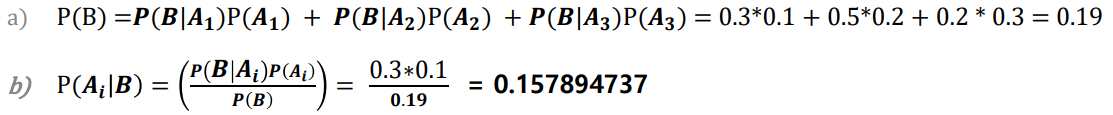
2. 확률 변수
확률 변수(random variable)
- 표본공간에서 각 사건에 실수를 대응시키는 함수를 확률 변수라고 함
- 확률 변수의 값은 하나의 사건에 대하여 하나의 값을 가지며, 실험의 결과에 의하여 변함
- 일반적으로 확률 변수는 대문자로 표현하며, 확률변수의 특정값을 소문자로 표현함
* 확률 변수: X, Y 등 대문자 표현
* 확률 변수의 특정값: x, y등 소문자로 표현
* 이산 확률 변수(discrete random variable): 셀 수 있는 값들로 구성되거나 일정 범위로 나타나는 경우
* 연속 확률 변수(continuous random variable): 연속형 또는 무한대와 같이 셀 수 없는 경우
확률 변수 예시
(a) 반도체 1000개의 wafer중 불량품의 수 X
(b) 공장에서 생산하는 전구의 수명 T
(c) 주사위를 던질 때 나오는 눈의 수 V
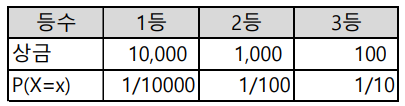
확률 변수의 평균 : 기대값 이라고 표현하기도 하며, 수식은 아래와 같음
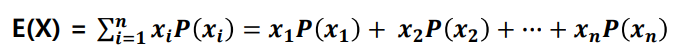
주사위를 던졌을때의 기대값은
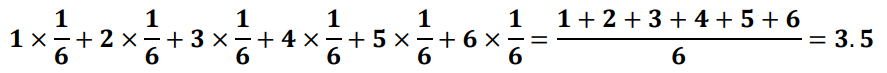
확률 변수의 분산
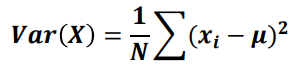
기대값의 성질
a, b가 상수이고, X, Y를 임의의 확률 변수라고 할 때 다음이 성립한다.
(a) E(a) = a
(b) E(aX) = aE(X)
(c) E(aX+b) = aE(X) + b
(d) E(aX±bY) = αE(X) ± bE(Y)
(e) X, Y가 독립 일때 E(XY) = E(X) E(Y)
분산의 성질
a, b가 상수이고, X, Y를 임의의 확률 변수라고 할 때 다음이 성립한다.
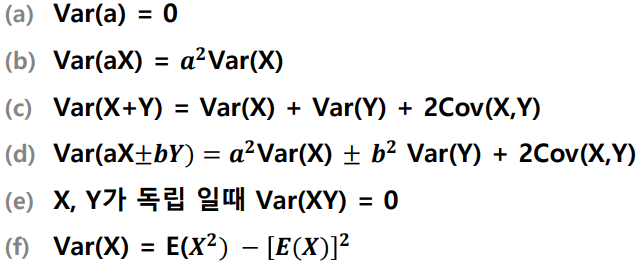
공분산
2개의 확률변수의 선형 관계를 나타내는 값으로, 하나의 값이 상승할 때 다른 값도 상승한다면, 양의 공분산을 가지고
반대로 하나의 값이 상승할 때 하락한다면 음의 공분산을 가짐
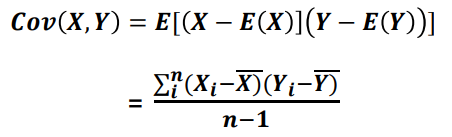




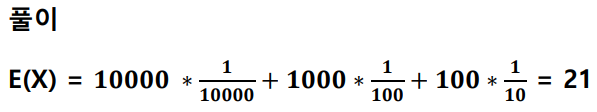
'데이터 분석 > 통계' 카테고리의 다른 글
| [통계]모집단과 표본 분포 1)모집단과 표본 (0) | 2023.11.14 |
|---|---|
| [통계]확률 이론 2) 연속형 확률 분포 (1) | 2023.11.14 |
| [통계]확률 이론 1) 이산형 확률 분포 (1) | 2023.11.14 |
| [통계]데이터의 이해 (1) | 2023.11.14 |
| [통계]기초 통계학 개요 (0) | 2023.11.14 |




