RUBY
[통계]데이터의 이해 본문
통계
2. 데이터의 이해
데이터에 대한 이해와 기초적인 통계량에 대한 설명
1. 데이터와 그래프
변수(Variable)
- 수학에서의 변수란, 어떤 정해지지 않은 임의의 값을 표현하기 위해 사용된 '기호' 이다. 보통 쉽게 설명하기 위해서 '변하는 숫자' 라는 표현을 자주 쓰고는 한다.
- 통계학에서는 조사 목적에 따라 관측된 자료값을 변수라고 함, 해당 변수에 대하여 관측된 값들이 바로 자료(Data)가 됨
질적 자료
- 관측된 데이터가 성별, 주소지(시군구), 업종 등과 같이 몇 개의 범주로 구분하여 표현할 수 있는 데이터를 의미함
- 데이터 입력시 1은 남자, 2는 여자로 표현 가능하나 여기서 숫자의 의미는 없음 (순서형 변수: 교육수준, 건강상태)
양적 자료
- 관측된 데이터가 숫자의 형태로 숫자의 크기가 의미를 갖고 있음
- 숫자를 표현할 때는 이산형 데이터와 연속형 데이터로 구분할 수 있음

데이터를 분석하는 과정 중에 가장 많이 사용하는 분석 방법을 Exploratory Data Analysis 라고함
EDA는 데이터를 탐색하는 분석 방법으로 도표, 그래프, 요약 통계 등을 사용하여 데이터를 체계적으로 분석하는 하나의 방법임
목적
- 데이터 분석 프로젝트 초기에 가설을 수립하기 위해 사용
- 데이터 분석 프로젝트 초기에, 적절한 모델 및 기법의 선정
- 변수 간 트렌드, 패턴, 관계 등을 찾고 통계적 추론을 기반으로 가정을 평가
- 분석 데이터에 적절한가 평가, 추가 수집, 이상치 발견 등에 활용
데이터 시각화(data visualization)는 데이터 분석 결과를 쉽게 이해할 수 있도록 시각적으로 표현하고 전달되는 과정을 말한다. 데이터 시각화의 목적은 도표(graph)라는 수단을 통해 정보를 명확하고 효과적으로 전달하는 것이다.
| 구분 | 주요 시각화 방법 |
| 시간 시각화 | 막대 그래프, 누적 막대 그래프, 점 그래프 |
| 분포 시각화 | 파이 차트, 도넛 아트, 트리맵, 누적 연속 그래프 |
| 관계 시각화 | 스캐터플롯, 버플차트, 히스토그램 |
| 비교 시각화 | 히트맵, 스타 차트, 평행 좌표계, 다차원 턱도법 |
| 공간 시각화 | 지도 맵핑 |

2. 데이터의 기초 통계량
기초 통계량
- 통계량(statistic)은 표본으로 산출한 값으로, 기술 통계량이라고도 표현함
- 통계량을 통해 데이터(표본)가 갖는 특성을 이해 할 수 있음
중심 경향치
- 표본(데이터)를 이해하기 위해서는 표본의 중심에 대해서 관심을 갖기 때문에 표본의 중심을 설명하는 값을 대표값이라 하며 이를 중심경향치라고 함
- 대표적인 중심 경향치는 평균이며, 중앙값, 최빈값, 절사 평균 등이 있음
▶ 평균은 모집단으로 부터 관측된 n개의 x가 주어 졌을때 아래와 같이 정의됨

▶ 평균은 표본으로 추출된 표본 평균(sample mean)이라고하며, 모집단의 평균을 모평균이라고 한다.
| 표준 평균 표기법 | |
| 모평균 표기법 |
중앙값(median)
- 평균과 같이 자주 사용하는 값으로 표본으로 부터 관측치를 크기순으로 나열 했을 때, 가운데 위치하는 값을 의미함
- 관측치가 홀수 일 경우 중앙에 취하는 값이고, 짝수 일 경우 가운데 두개의 값을 산술 평균한 값임
- 이상치가 포함된 데이터에 대해서 사용함
관측치를 크기순으로 X(1), X(2), … ,X(n) 나열 했을 때, 중앙값 m은
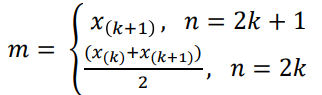
ex) 80, 82, 84, 85, 90, 95, 100 : 85
80, 82, 84, 85, 90, 95, 95, 100 : 87.5
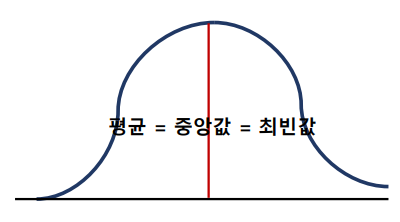
최빈값(mode)
- 관측치 중에서 가장 많이 관측되는 값
- 옷사이즈와 같이 명목형 데이터의 경우 사용
 |
 |
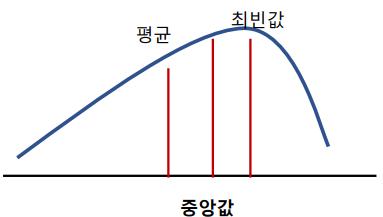 |
| A. 대칭 분포 | B. 오른쪽 꼬리가 김 | C. 왼쪽 꼬리가 김 |
산포도
- 데이터가 어떻게 흩어져 있는지를 확인하기 위해서는 중심경향치와 함께 산포에 대한 측도를 같이 고려해야 함
- 데이터의 산포도를 나타내는 측도로는 범위, 사분위수, 분산, 표준편차, 변동 계수 등이 있음
범위(Range)
- 데이터의 최대값과 최소값의 차이를 의미함
사분위수(quartile)
- 전체 데이터를 오름차순으로 정렬하여 4등분을 하였을 때, 첫 번째를 제1사분위수(Q1), 두 번째를 제2사분위수(Q2), 세 번째를 제3사분위수(Q3)이라고 함
- 사분위수 범위(interquartile range): IQR = 제 3사분위수(Q3) – 제1사분위수(Q1)
백분위수(percentile)
- 전체 데이터를 오름차순으로 정렬하여 주어진 비율에 의해 등분한 값을 말하며, 제p백분위수는 p%에 위치한 자료 값을 말함
- 데이터를 오름차수로 배열하고 자료가 n개가 있을 때, 제(100*p) 백분위수는 아래와 같음
1) np가 정수이면, np번째와 (np + 1)번째 자료의 평균
2) np가 정수가 아니면, np보다 큰 최소의 정수를 m이라고 할 때 m번째 자료
분산(variance)
- 데이터의 분포가 얼마나 흩어져 있는지를 알 수 있는 측도임
- 데이터의 각각의 값들의 편차 제곱합으로 계산하며 수식은 아래와 같음
| 표본 분산 |  |
표준 편차(standard deviation)
- 분산의 제곱근으로 정의하며 수식은 아래와 같음
| 표본 표준 편차 |  |
분산
- 크기가 N인 모집단의 평균을 라고 할 때 모평균과 모분산은 다음과 같음
| 모분산 |  |
| 모표준편차 | 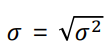 |
변동계수(Coefficient of Variation: CV)
- 평균이 다른 두개 이상의 그룹의 표준편차를 비교할 때 사용함
- 변동계수는 표준편차를 평균으로 나누어서 산출하여 단위나 조건에 상관 없이 서로 다른 그룹의 산포를 비교하며 실제 분석에서 자주 사용함
| 변동계수 |  |
| 정규 분포 모양: 평균과 분산에 따라서 모양이 달라짐 | 분산이 크면 분포가 넓어지고 분산이 작으면 분포가 좁아짐 |
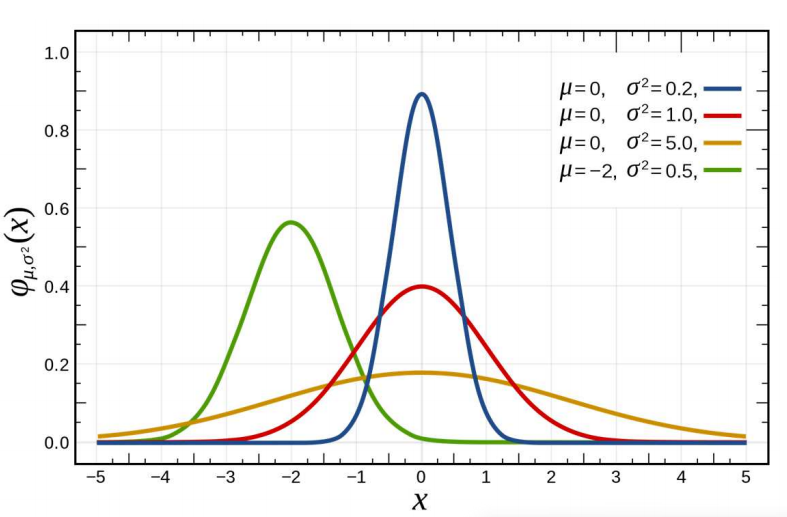 |
 |
왜도(skew)
- 자료의 분포가 얼마나 비대칭적인지 표현하는 지표임
- 왜도가 0이면 좌우가 대칭이고, 0에서 클수록 우측꼬리가 길고 0에서 작을수록 좌측 꼬리가 김
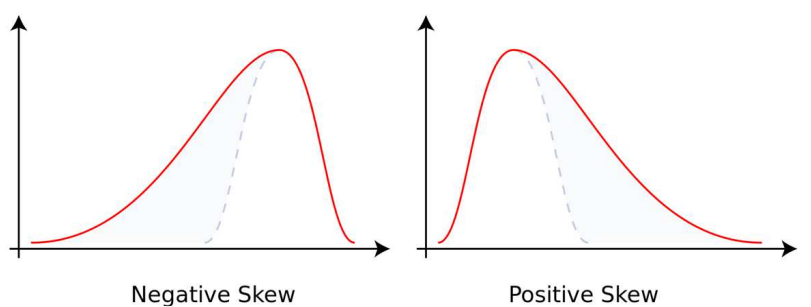
첨도(kurtosis)
- 확률분포의 꼬리가 두꺼운 정도를 나타내는 척도임
- 첨도값(K)이 3에 가까우면 산포도가 정규분포에 가까움
- 3보다 작을 경우에는(K<3) 산포는 정규분포보다 꼬리가 얇은 분포로 생각할 수 있다, 첨도값이 3보다 큰 양수이면(K>3) 정규분포보다 꼬리가 두꺼운 분포로 판단

'데이터 분석 > 통계' 카테고리의 다른 글
| [통계]모집단과 표본 분포 1)모집단과 표본 (0) | 2023.11.14 |
|---|---|
| [통계]확률 이론 2) 연속형 확률 분포 (1) | 2023.11.14 |
| [통계]확률 이론 1) 이산형 확률 분포 (1) | 2023.11.14 |
| [통계]확률 이론 (0) | 2023.11.14 |
| [통계]기초 통계학 개요 (0) | 2023.11.14 |